Quick Start Tutorial

This notebook shows an example Exploratory Data Analysis utilizing data-describe.

Note: Part of this notebook uses optional dependencies for text analysis. To install these dependencies, run pip install data-describe[nlp]

[1]:

import data_describe as dd

Data

This tutorial uses toy datasets from sklearn.

[2]:

from sklearn.datasets import load_boston
import pandas as pd

[3]:

dat = load_boston()
df = pd.DataFrame(dat['data'], columns=dat['feature_names'])
df['price'] = dat['target']

[4]:

df.head()

[4]:
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT price
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2

Data Overview

Column Descriptions:

  • CRIM per capita crime rate by town

  • ZN proportion of residential land zoned for lots over 25,000 sq.ft.

  • INDUS proportion of non-retail business acres per town

  • CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)

  • NOX nitric oxides concentration (parts per 10 million)

  • RM average number of rooms per dwelling

  • AGE proportion of owner-occupied units built prior to 1940

  • DIS weighted distances to five Boston employment centres

  • RAD index of accessibility to radial highways

  • TAX full-value property-tax rate per $10,000

  • PTRATIO pupil-teacher ratio by town

  • B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town

  • LSTAT % lower status of the population

  • MEDV Median value of owner-occupied homes in $1000’s

[5]:

df.shape

[5]:

(506, 14)

First we inspect some of the overall statistics about the data. Some examples of interesting things to note: - 93% of CHAS are the same value, zero - ZN also has a high amount of zeros - The mean of TAX is significantly higher than the median, suggesting this is right-skewed

[6]:

dd.data_summary(df)
Info
Rows 506
Columns 14
Size in Memory 55.5 KB
Data Type Nulls Zeros Min Median Max Mean Standard Deviation Unique Top Frequency
CRIM float64 0 0 0.0063 0.26 88.98 3.61 8.59 504 2
ZN float64 0 0 0 0 100 11.36 23.30 26 372
INDUS float64 0 0 0.46 9.69 27.74 11.14 6.85 76 132
CHAS float64 0 0 0 0 1 0.069 0.25 2 471
NOX float64 0 0 0.39 0.54 0.87 0.55 0.12 81 23
RM float64 0 0 3.56 6.21 8.78 6.28 0.70 446 3
AGE float64 0 0 2.90 77.50 100 68.57 28.12 356 43
DIS float64 0 0 1.13 3.21 12.13 3.80 2.10 412 5
RAD float64 0 0 1 5 24 9.55 8.70 9 132
TAX float64 0 0 187 330 711 408.24 168.37 66 132
PTRATIO float64 0 0 12.60 19.050 22 18.46 2.16 46 140
B float64 0 0 0.32 391.44 396.90 356.67 91.20 357 121
LSTAT float64 0 0 1.73 11.36 37.97 12.65 7.13 455 3
price float64 0 0 5 21.20 50 22.53 9.19 229 16 
None

[6]:

data-describe Summary Widget

We can also look at a visual representation of the data as a heatmap:

[7]:

dd.data_heatmap(df)
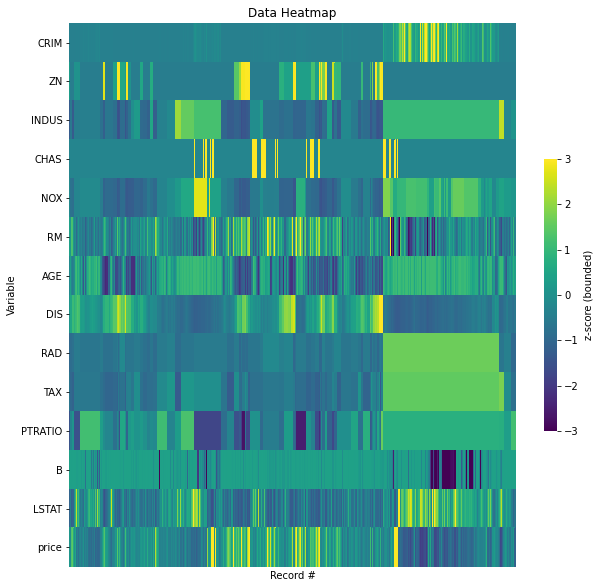
../_images/_notebooks_quick_start_12_0.png 
[7]:

Heatmap Widget showing standardized values.

There are some sections of the data which have exactly the same values for some columns. For example, RAD = 1.661245 between record number 356 ~ 487. Similar patterns appear for INDUS and TAX. Is this a sorting issue or is there something else going on? Some additional investigation into data collection may answer these questions.

We can also look at the correlations:

[8]:

dd.correlation_matrix(df)

<AxesSubplot:title={'center':'Correlation Matrix'}>

[8]:

<data_describe.core.correlation.CorrelationWidget at 0x26b44cc2b48>
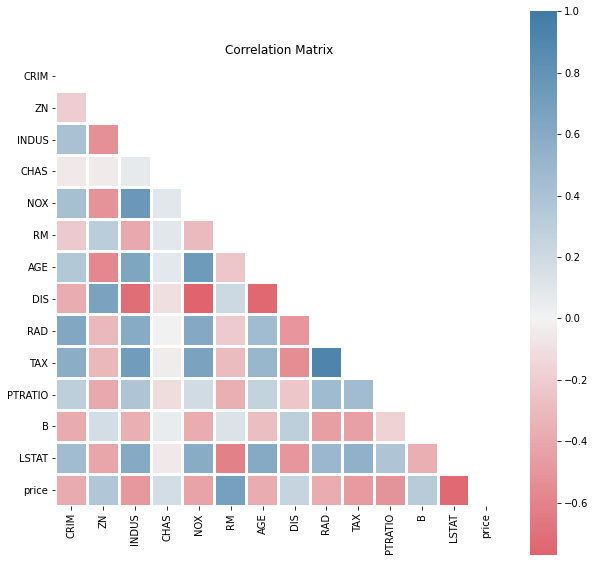
../_images/_notebooks_quick_start_15_2.png

Features like AGE and DIS appear to be inversely correlated. CHAS doesn’t appear to have strong correlation with any other feature.

It might also help to re-order the features for comparisons using the cluster argument.

[9]:

dd.correlation_matrix(df, cluster=True)

<AxesSubplot:title={'center':'Correlation Matrix'}>

[9]:

<data_describe.core.correlation.CorrelationWidget at 0x26b44814f48>
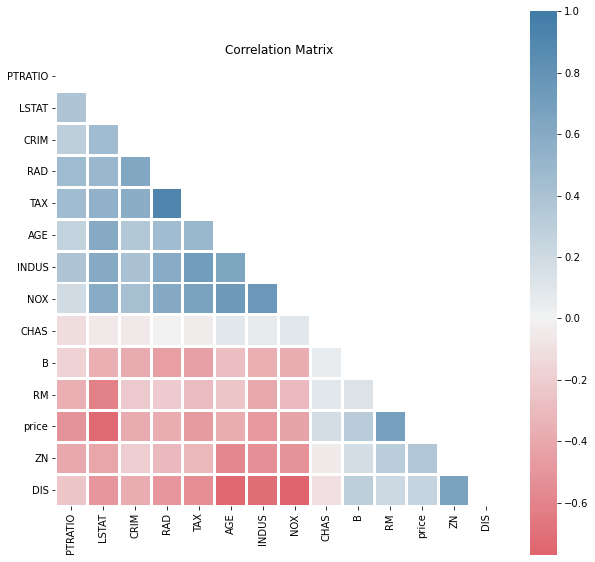
../_images/_notebooks_quick_start_17_2.png

From this plot we can observe there are are two groups of inversely related features: PTRATIO to NOX and B to DIS.

Data Inspection

We can also do some more detailed inspection of individual features.

We can show histograms and violin plots of each numeric feature using the dd.distribution function.

[10]:

from IPython.display import display
# display is used to show plots from inside a loop
for col in df.columns:
    display(dd.distribution(df, plot_all=True).plot_distribution(col))
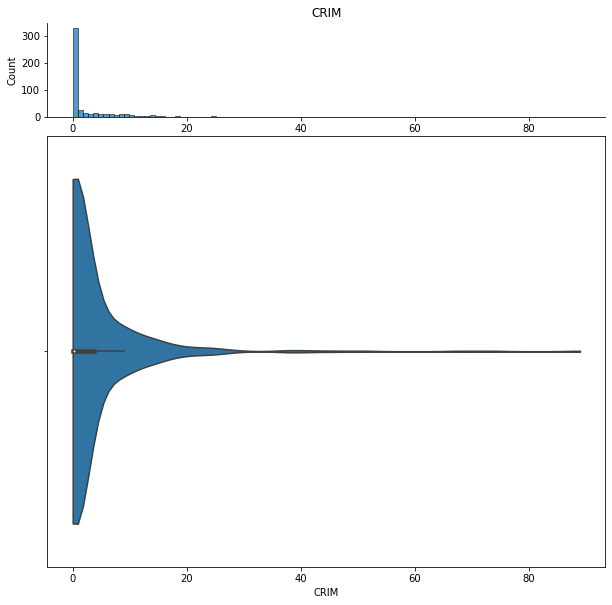
../_images/_notebooks_quick_start_21_0.png
../_images/_notebooks_quick_start_21_1.png
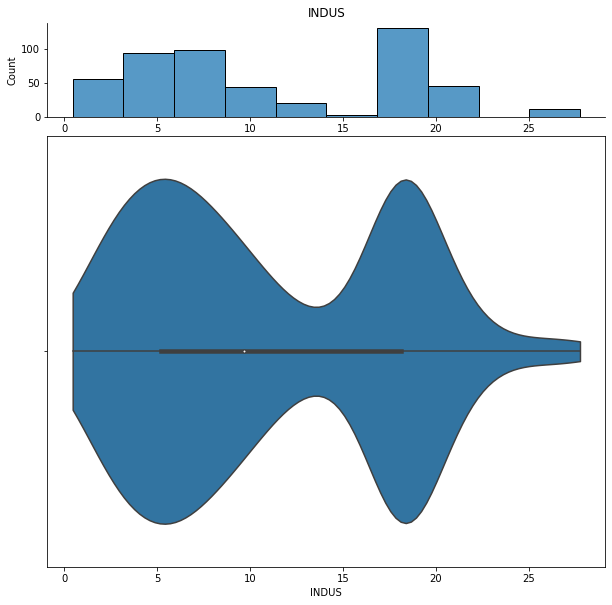
../_images/_notebooks_quick_start_21_2.png
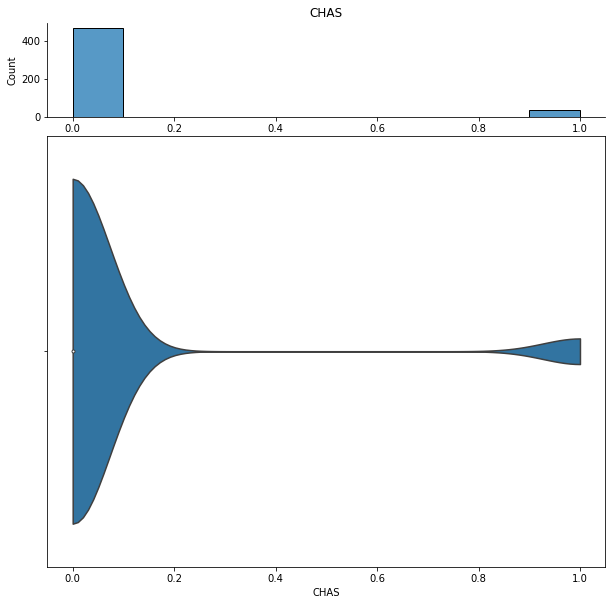
../_images/_notebooks_quick_start_21_3.png
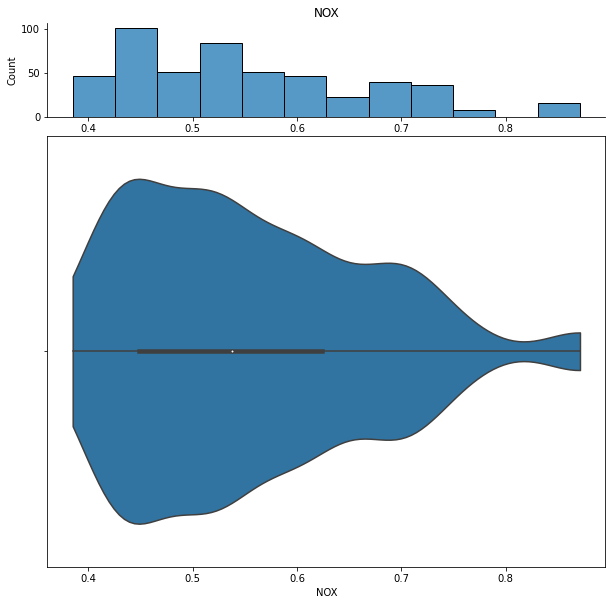
../_images/_notebooks_quick_start_21_4.png
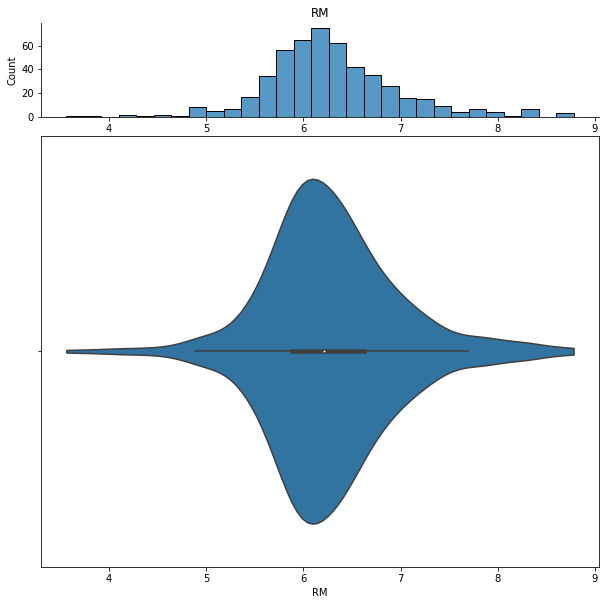
../_images/_notebooks_quick_start_21_5.png
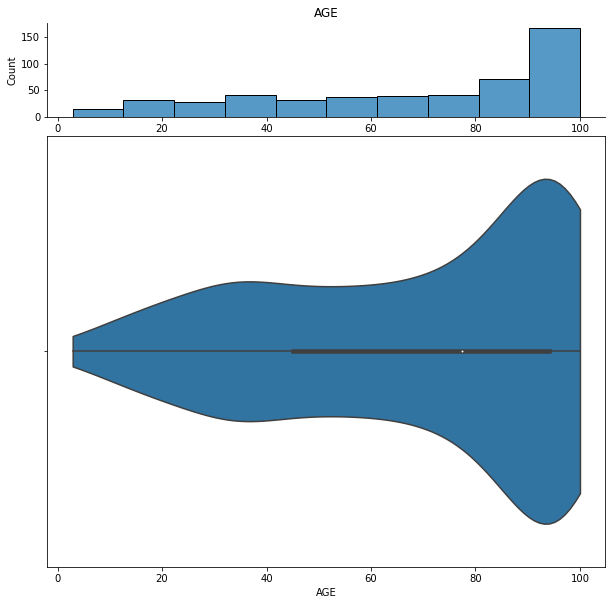
../_images/_notebooks_quick_start_21_6.png
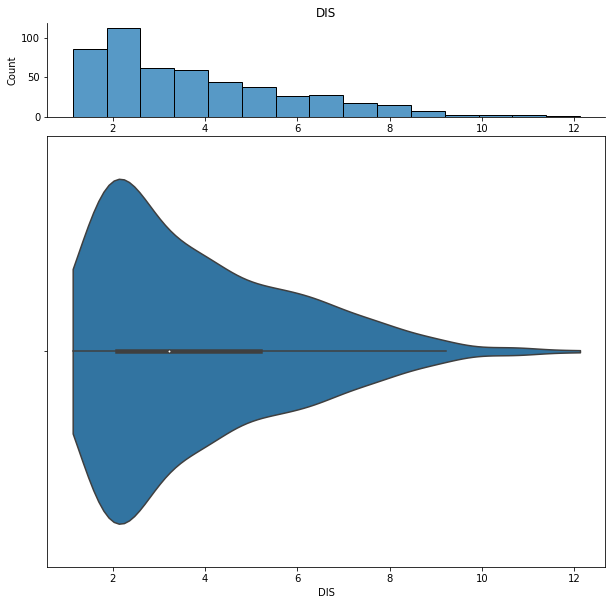
../_images/_notebooks_quick_start_21_7.png
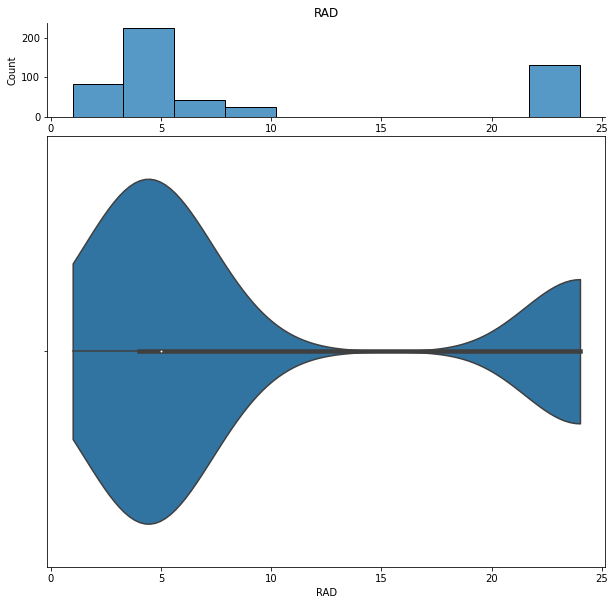
../_images/_notebooks_quick_start_21_8.png
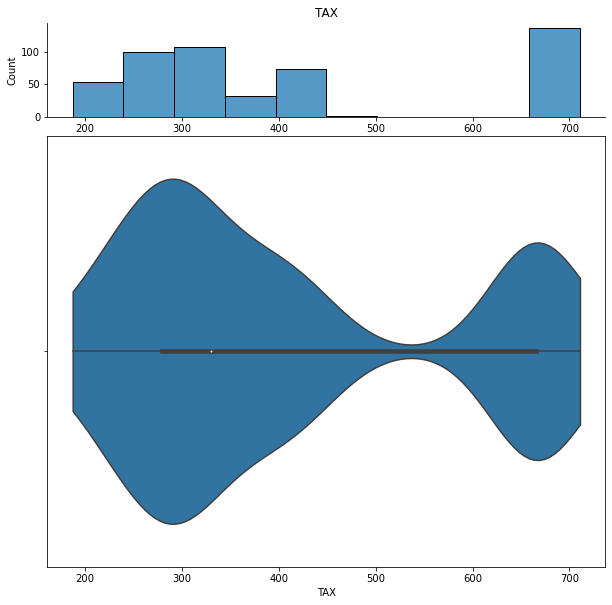
../_images/_notebooks_quick_start_21_9.png
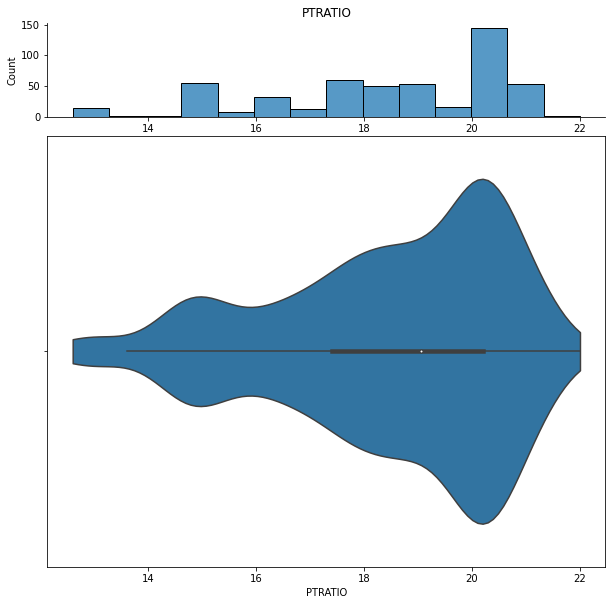
../_images/_notebooks_quick_start_21_10.png
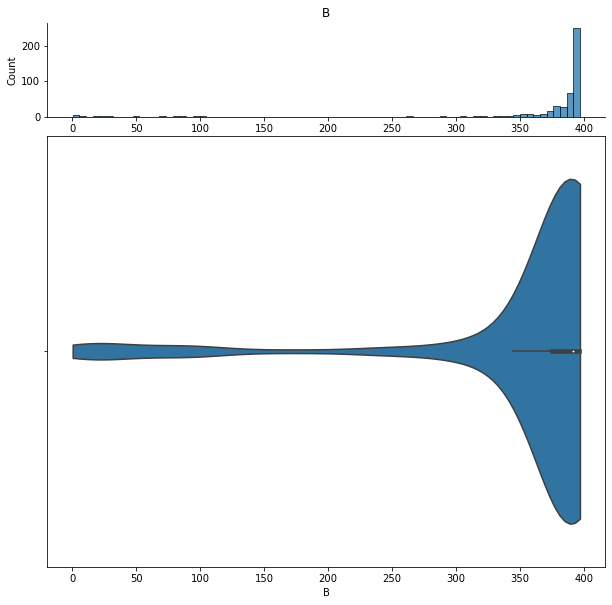
../_images/_notebooks_quick_start_21_11.png
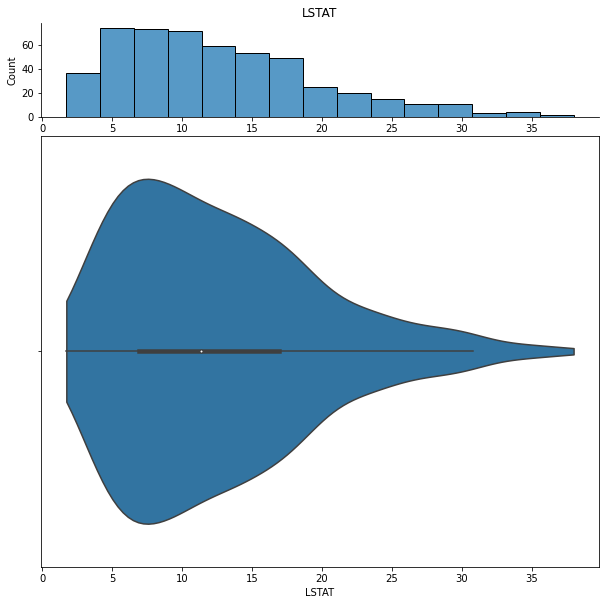
../_images/_notebooks_quick_start_21_12.png
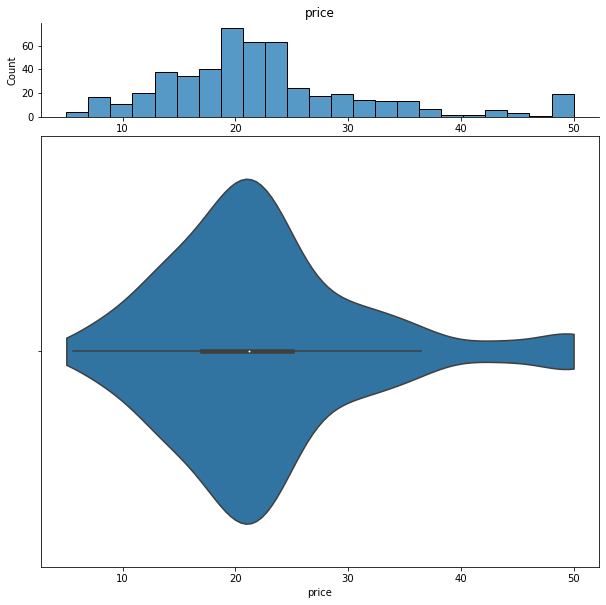
../_images/_notebooks_quick_start_21_13.png

We can also look at bivariate distributions using scatter plots. In addition to plotting all pairs in a scatterplot matrix, we can also specify a filter for certain scatterplot diagnostic features.

[11]:

dd.scatter_plots(df, plot_mode='matrix')

<seaborn.axisgrid.PairGrid at 0x26b44e40188>

[11]:

data-describe Scatter Plot Widget
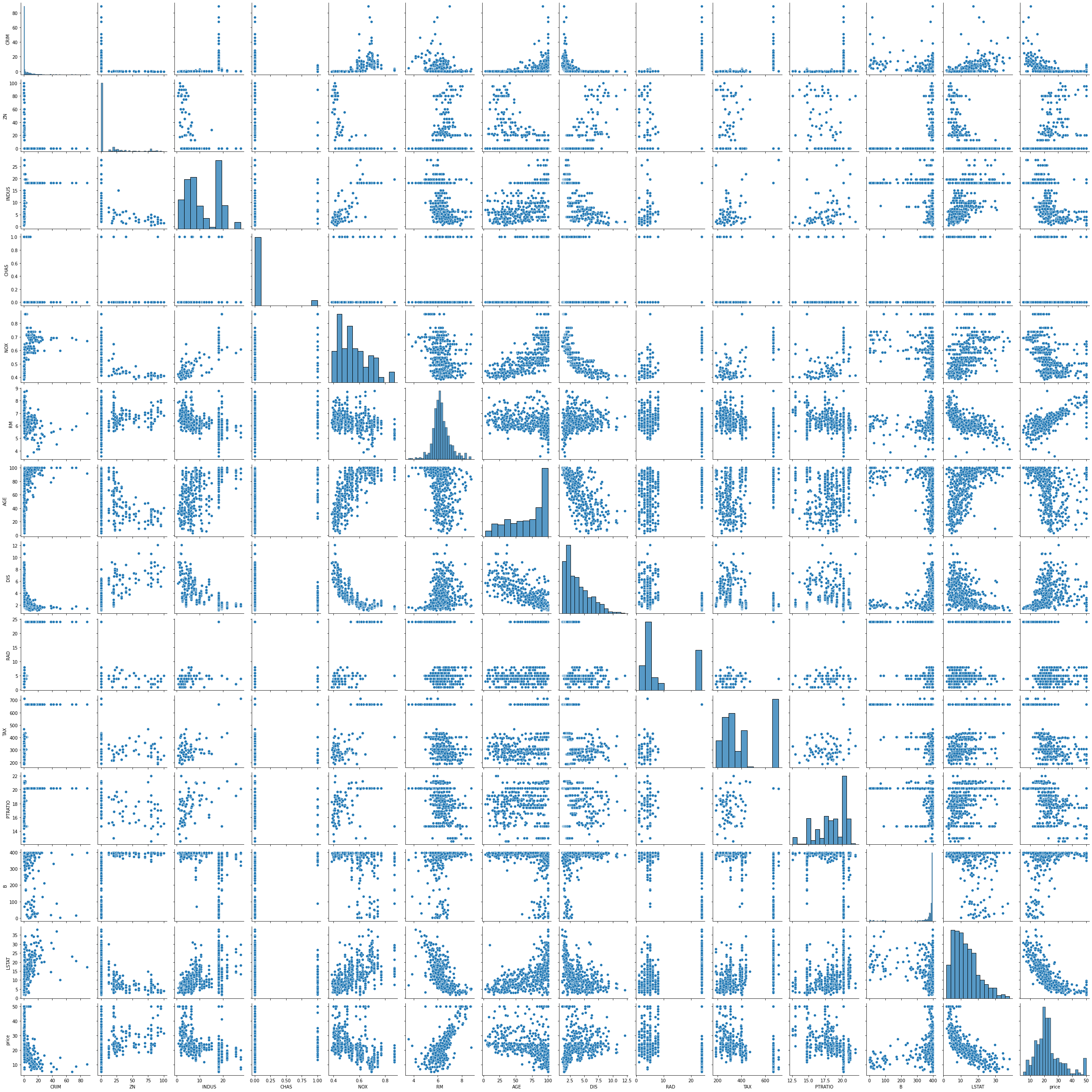
../_images/_notebooks_quick_start_23_2.png 
[12]:

dd.scatter_plots(df, threshold={'Outlier': 0.9})

<seaborn.axisgrid.PairGrid at 0x26b4dae2388>

[12]:

data-describe Scatter Plot Widget
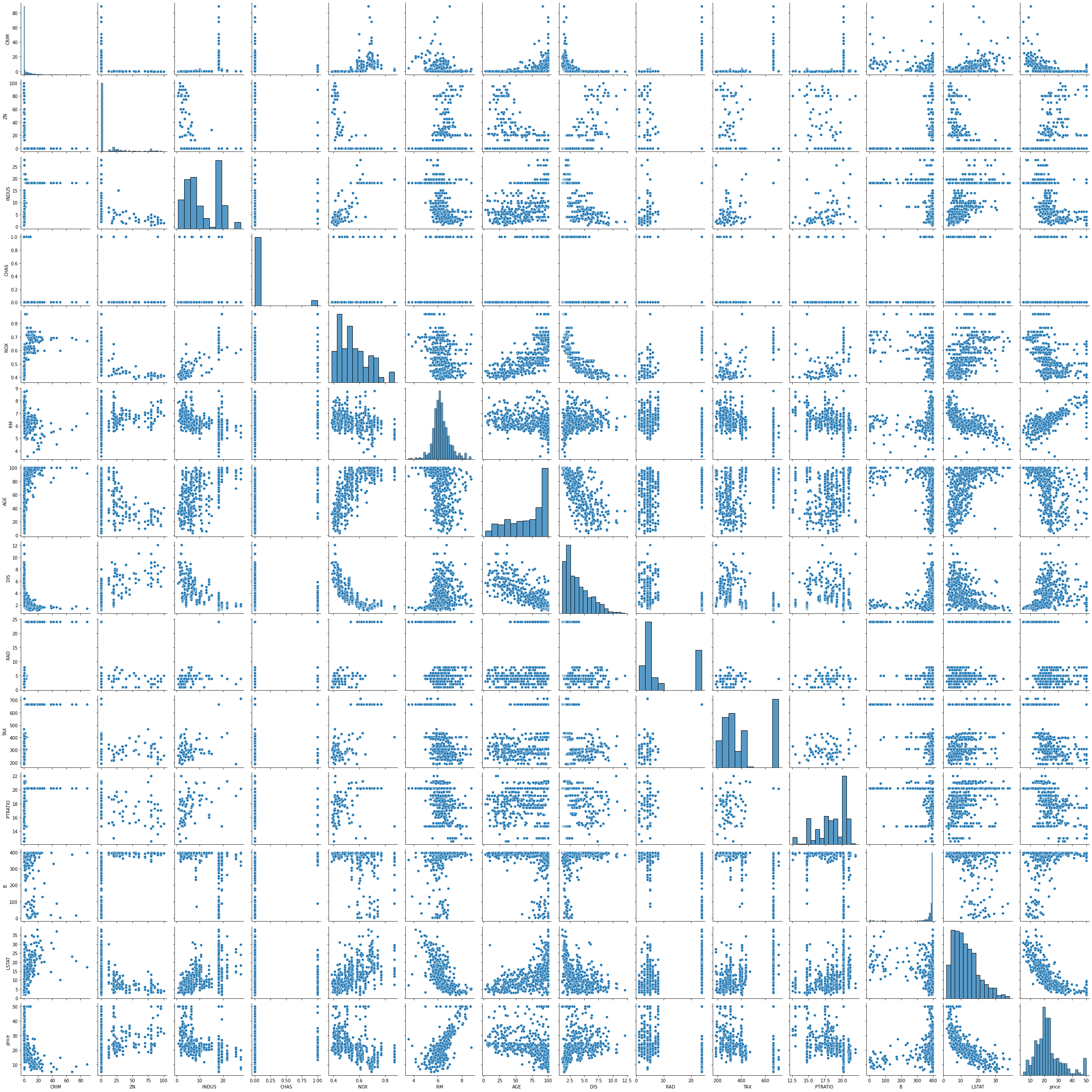
../_images/_notebooks_quick_start_24_2.png

Advanced Analysis

In addition to general plots, we can also use some advanced analyses as shown below.

Cluster Analysis

What segments or groups are present in the data?

[13]:

dd.cluster(df)

<AxesSubplot:title={'center':'kmeans Cluster'}, xlabel='Component 1 (47.0% variance explained)', ylabel='Component 2 (12.0% variance explained)'>

[13]:

Cluster Widget using kmeans
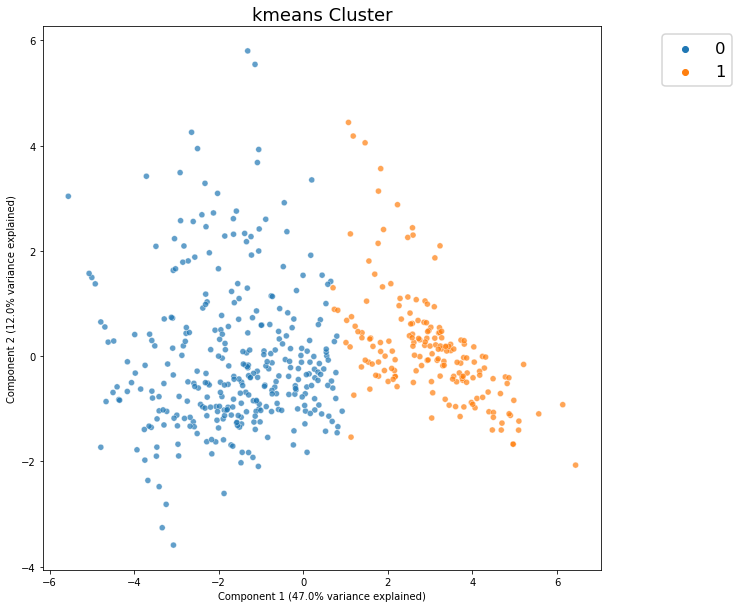
../_images/_notebooks_quick_start_27_2.png

From this plot, we see that there does not appear to be strongly distinct clusters in the data.

Feature Importance

Which features are most predictive of price? We use Random Forest as a baseline model to test for importance.

[14]:

from sklearn.ensemble import RandomForestRegressor

[15]:

dd.importance(df, 'price', estimator=RandomForestRegressor(random_state=42))

[15]:

Text(0.5, 1.0, 'Feature Importance')
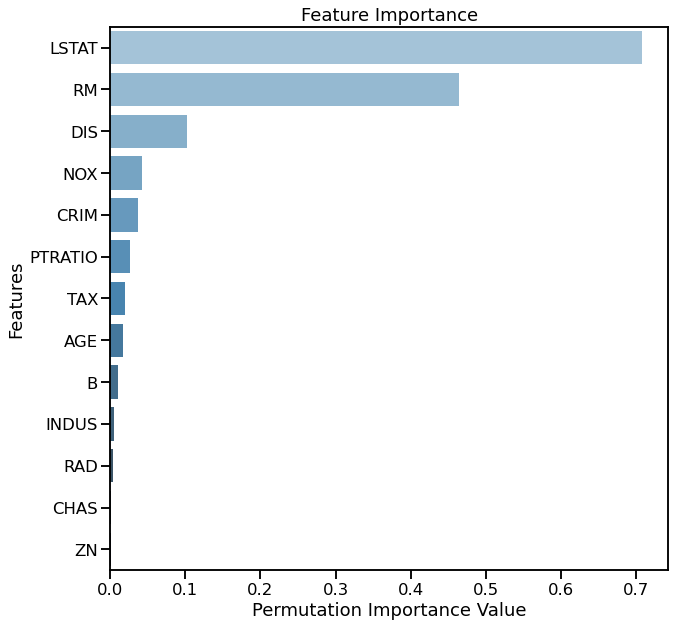
../_images/_notebooks_quick_start_32_1.png

It appears that LSTAT and RM are most important for predicting price.

Topic Modeling

Since the Boston housing data set does not contain textual features, the 20 newsgroups text dataset is used to demonstrate the Topic Modeling widget.

[16]:

from sklearn.datasets import fetch_20newsgroups

[17]:

dat = fetch_20newsgroups(subset='test')
df2 = pd.DataFrame({'text': dat['data']})
df2 = df2.sample(150)

[18]:

df2.head()

[18]:
text
1779 From: penev@rockefeller.edu (Penio Penev)\nSub...
5598 From: mathew <mathew@mantis.co.uk>\nSubject: R...
4313 From: dps@nasa.kodak.com (Dan Schaertel,,,)\nS...
97 From: sinn@carson.u.washington.edu (Philip Sin...
6225 From: smn@netcom.com (Subodh Nijsure)\nSubject...

Text preprocessing can be applied before topic modeling to improve accuracy.

[19]:

from data_describe.text.text_preprocessing import preprocess_texts, bag_of_words_to_docs
processed = preprocess_texts(df2['text'])
text = bag_of_words_to_docs(processed)

[20]:

from data_describe.text.topic_modeling import topic_model

[21]:

lda_model = topic_model(text, num_topics=3)
lda_model
Topic 1 Topic 1 Coefficient Value Topic 2 Topic 2 Coefficient Value Topic 3 Topic 3 Coefficient Value
Term 1 two 0.023 god 0.045 etc 0.022
Term 2 use 0.020 us 0.021 help 0.022
Term 3 .. 0.018 also 0.017 also 0.022
Term 4 computer 0.018 use 0.014 two 0.020
Term 5 anyone 0.017 work 0.014 may 0.018
Term 6 right 0.014 way 0.014 back 0.016
Term 7 think 0.014 see 0.013 think 0.016
Term 8 game 0.014 many 0.013 make 0.016
Term 9 system 0.014 think 0.013 take 0.015
Term 10 way 0.014 well 0.012 well 0.015 
[21]:

<data_describe.text.topic_modeling.TopicModelWidget at 0x26b40933208>